진법(위치값 기수법)의 의미, 그리고 2진법, 8진법, 16진법, 10진법 변환 원리와 방법
목차
1. 진법이란
2. x진법(2진법, 8진법, 16진법, 10진법)
3. 진법 간 변환 원리, 방법
- x진수 → 10진수
- 10진수 → x진수
- 2진수 ↔ 16진수
들어가기에 앞서
오늘은 진법에 대해 공부한 내용을 정리해 본다. 진법은 그동안 꼭 한 번은 확실하게 짚고 넘어가야지 했던 개념이다. 진법이란 무엇인가에 대한 기본 정의와 2, 8, 16, 10진법 각각에 대하여 살펴보았다. 또한, 진법 변환을 어떤 방식으로 하며 이에 대해 어떻게 생각하면 좋을지 적어본 글이다. 진법 변환에 관한 내용은 좀 길다. 풀어내는 과정과 설명을 가능한 꼼꼼히 적어두었기 때문이다.
1. 진법이란
- 진법의 정의
우리가 흔히 알고있는 10진법, 2진법 등은 위치값 기수법(positional system)이라는 수의 표현법이다. 기수법은 수를 눈으로 볼 수 있게 표현한 방법이며, 이중 하나인 위치값 기수법은 숫자의 위치와 계수를 이용하여 수를 나타내는 방법이다. 아주 오랜 옛날부터 수를 표현하기 위해 다양한 기수법이 고안되어 왔으며, 현대에서 기수법이라 하면 일반적으로 위치값 기수법을 의미한다고 한다. 말이 어렵다.
이 위치값 기수법 중 우리를 포함한 현대인이 대표적으로 사용하는 체계가 바로 10진법이다. 10진법에서는 0~9까지가 한 자릿수에 표현되며 9를 초과하여 10이 되면 자리올림이 발생한다. 컴퓨터가 대표적으로 사용하는 2진법은 한 자릿수에 0,1만 표현되며 1을 초과하여 2가 되면 자리올림이 발생한다. 결국 x진법은 x를 기준으로 자리올림하는 표현법이다.
- 예시로 살펴보는 진법의 정의 풀이
위치값 기수법에 대해 조금 더 살펴보자
10진수 6491(육천사백구십일)은 아래와 같은 식으로 표현할 수 있다.(진수: 진법들의 숫자)

10진수 6491은 10을 기준으로 자릿수가 오르고 있다. 이를 표현한 위 식 중 가장 마지막 줄을 보자. 기수 10이 10³ 10² 10¹ 10⁰ 으로 등급화되었다. 즉, 10의 거듭제곱들이 10의 계수(階數, rank)가 된다. 이때 숫자의 위치에 따라 10의 계수(등급)를 표현하였으므로 '숫자의 위치 = 계수'다.
(주의, 앞의 '계수'와 뜻이 다른 '계수'가 하나 더 등장한다.)
6천4백9십1에서 계수(係數, coefficient) 6, 4, 9, 1은 해당 위치의 계수(階數, rank) 10ⁿ의 개수를 나타내는 숫자다.(한자 거지같네 신발) 계수(係數, coefficient) 6, 4, 9, 1에 따라 1000이 6개, 100이 4개, 10이 9개 1이 1개 있다고 말할 수 있다.
위에서 살펴본 위치값 기수법의 정의에 대해 다시 한번 생각해 보자. 6491은 숫자의 위치로 10의 등급(거듭제곱)을 표현하면서 계수(係數, coefficient) 6, 4, 9, 1을 이용해 각 10의 거듭제곱들의 개수를 표현한 수다. 즉, '숫자의 위치와 계수를 이용하여 수를 나타내는 방법'이라는 정의가 성립한다.
- 일반화와 진법의 활용
수식으로는 아래와 같이 표현된다.

이때 x가 위의 10진수 6491에서의 10과 같이 등급화된 기수이다. x가 2이면 2진법, 3이면 3진법, 16이면 16진법, 60이면 60진법이 된다. a는 xⁿ의 개수를 표현한 계수(係數, coefficient) 다.
각각의 진법들은 용도에 따라 다양한 곳에서 사용된다. 10진법은 우리 현대사회에서 가장 일반적으로 사용하는 기수법이며, 컴퓨터 분야에서는 2진법과 16진법을, 시간은 60진법과 12진법을 대표적으로 사용한다.
2. x진법
많이 사용되는 순서대로 10진법, 2진법, 16진법, 8진법에 대해 살펴보고자 한다.
- 10진법 decimal
현대에서 가장 일반적으로 사용되고 있는 기수법이다. 한 자리에 0부터 9까지의 숫자가 표현된다. 한자리의 수가 10이 될 때마다 자리올림이 발생한다. 십진법은 사람 손가락 개수에서 유래되었다고 한다.
- 표현
다른 진법과 구분하여 표현해야 할 때는 아래첨자로 10이나 A를 붙여 쓸 수 있다.

- 식

- 예시

- 2진법 binary
0과 1로만 수를 표현한다. 한 자리에 0과 1만 올 수 있으며 2가 되는 순간 자리올림이 발생한다. 컴퓨터 등의 전자기기에서 전기 신호의 꺼짐(0)과 켜짐(1)을 표현할 수 있기 때문에 유용하게 사용된다.
- 표현
다른 기수법과 구분해야 할 땐 아래첨자로 2를 붙이거나 이진수 뒤에 b를 쓰거나, 이진수 앞에 0b를 붙여 표현할 수 있다.

- 식
십진수로 식을 표현하면 아래와 같다.

- 위쪽에서 위치값 기수법에 대해 정의했던 것처럼 2ⁿ은 거듭제곱이고, 등급화된 수이다. 그리고 b는 2ⁿ의 개수를 표현하고 있다. bn2ⁿ 은 뒤에서 (n+1) 번째 자리에 2의 n제곱이 bn개 있는 것이다. 예를 들어 b₆2⁶은 뒤에서 7번째 자리에 2의 6제곱(=2의 6승)이 b₆개 있는 것이다. 2진수에서 한 자리에 올 수 있는 수는 0 또는 1 뿐이므로 b₆은 0 또는 1일 것이다.
- 예시

- 이진수 10010은 2의 4 제곱이 1개, 2의 1 제곱이 1개 있는 수이다. 위치값 기수법의 정의에 따라 숫자의 위치와 위치에 표현된 개수로 수가 표현된다.
- 16진법 hexadecimal
0~15가 한 자리에 표현되는 기수법이다. 16진수 1자리로 2진수 4자리를 표현할 수 있기 때문에 2진수를 사용하는 컴퓨터 분야에서 빼놓을 수 없는 기수법이다. 참고로 컴퓨터에서 2진수 8자리만큼의 메모리 공간의 단위를 1바이트라고 하는데 이를 16진수 2자리로 간단히 표현할 수 있는 것이다.
- 표현
0~9는 숫자로 표현하고 10~15는 알파벳 A~F를 사용한다. 십진수 10이 16진수 A로, 십진수 11이 16진수 B로, 10진수 15가 16진수 F로 표현된다. 십진수 1~15가 16진수로 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F 이렇게 표현되는 것이다. 숫자 뒤 아래첨자에 (16) 또는 hex를 붙여 16진수임을 나타낼 수 있다. 프로그래밍 언어 등에서는 0x를 앞에 붙이는 방식으로도 표현 가능하다.

- 식
십진수로 식을 표현하면 아래와 같다.

- 16ⁿ은 거듭제곱이고, 등급화된 수이다. 그리고 h는 16ⁿ의 개수를 표현하고 있다. hn16ⁿ 은 뒤에서부터 (n+1) 번째 자리에 16의 n제곱이 hn개 있는 것이다.
- 예시

- 십육진수 7F4CA 는 16의 4제곱이 7개, 16의 3제곱이 F개(F는 10진수로 15), 16의 제곱이 4개, 16이 C개(16진수로 12), 1이 A개(10진수로 10)인 수이다. 이 또한 위치값 기수법의 정의에 따라 숫자의 위치, 위치에 표현된 개수로 수를 시각적으로 표현한 것이다.
- 8진법 octal
한 자리에 0~7의 숫자를 표현할 수 있다. 8이 되면 자리올림이 발생한다. 10진법의 8은 8진법에서 10으로 표현된다. 마찬가지로 9(10) = 11(8), 10(10)=12(8)과 같이 표현된다. 8진법이라고 표현하지 않으면 10진법과 헷갈린다. 숫자 뒤에 8이나 알파벳 o를 붙여 표현한다고 한다. 0=0, 1=l, 2=s, 3=n, 4=m, 5=t, 6=f, 7=u 이런 식으로 숫자 대신 알파벳으로 표현하기도 한단다.(띠용) 컴퓨터에서 가끔 16진법 대신 사용된다고 한다. 나는 아직 본 적이 없다.
잘 안 쓰이니 표현, 수식 등은 패스하겠다.
3. 진법 간 변환 원리와 방법
이번에는 진법간 변환에 대해 살펴보자. 아래는 10진수로 0~30을 2, 8, 16진수로 변환한 표이다. 약간의 계산을 통해 아래의 변환을 직접 할 수 있다. 아래의 변환 방식은 위치값 기수법이라는 개념에 따라 여러 가지 방법으로 진법 변환을 해본 것이다. 인터넷에 있던 방식도 있고, 내 맘대로 해본 방식도 있다. 해서 이상할 수도

- x진법→10진법 변환
2진수, 8진수, 16진수 등의 수를 10진법으로 변환하는 방법은 앞서 계속 살펴본 바와 같다. x진법 수의 각 자리 숫자에 현재 자리의 위치만큼 x를 거듭제곱한 수를 곱한 뒤 모두 더해주면 된다. 말로 풀어내려니 너무 어렵다.. 아래 예시를 살펴보자
- 2진수 1001 → 10진수 변환

2진수 1001은 2의 3승이 1개, 2의 2승은 0개, 2의 1승이 0개, 2의 0승이 1개 있는 것이다. 따라서 맨 아랫줄과 같이 각각의 자리에 있는 숫자에 해당 위치만큼의 2의 거듭제곱을 곱하고 이들을 모두 더하면 9라는 10진수 결과가 나온다.
- 8진수 63 → 10진수 변환

8진수 63은 8의 1승이 6개, 8의 0승이 3개 있는 것이다. 8의 0승은 1이다. 따라서 맨 아랫줄과 같이 8의 1승과 6을 곱하고 8의 0승인 1과 3을 곱한 뒤 모두 더해주면 10진수 51이 나온다.
나머지 예시들을 직접 변환해 본 뒤 풀이를 살펴보는 방식을 취한다면 10진법으로의 변환에 대한 이해가 좀 더 쉽겠다.
- 111010(2), 1327(8), 25E(16), 5F2C9(16) → 10진수 변환
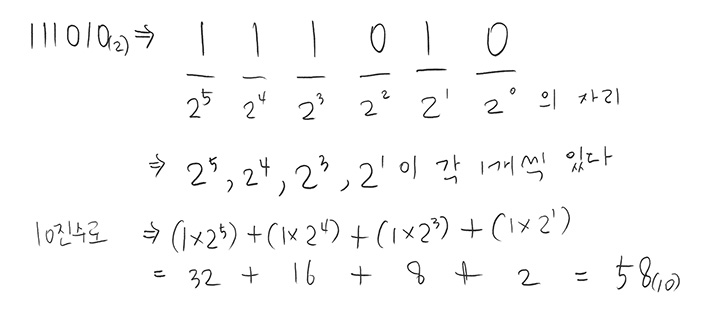



- 10진법→x진법 변환
10진법을 x진법으로 변환할 땐 나머지 연산을 이용할 수 있다. 10진수 13을 2진수로 변환하는 과정과, 5861을 16진수로 변환하는 과정을 아래에서 살펴보자. 여기에선 10진수를 2진수와 16진수로만 변환했지만 이 원리를 적용하면 10진법 수를 어떤 진수로도 변환할 수 있다.
- 10진수 13 → 2진수 변환
우선, 아래와 같이 2진수에서 1의 자리에 13이 통째로 들어있다고 생각해 보았다.

2진수는 하나의 자리에 0과 1만 올 수 있으며 2가 되는 순간 자리올림이 발생하는 수라고 하였다. 따라서 1의 자리에 있는 13은 다음 자리로 올라가야 한다. 13을 2로 나누면 몫은 6, 나머지는 1이 된다. (13 = 6x2+1) 따라서 몫인 6은 다음 자리로 올라가고 나머지 1만 1의 자리에 남는다. 아래처럼 말이다.

13은 2의 1승을 6개, 2의 0승을 1개 가진 수이다. 2의 0승 자리에 있던 13은 2로 나누어질 수 있는 수 12와 나머지 1로 떼어졌고, 이중 12는 는 2를 6개 가진 수로서 2의 1승 자리로 올라왔다.

다음으로 2의 1승 자리에 있는 6은 2보다 크므로 자리올림이 발생한다. 6을 2로 나누면 몫은 3, 나머지는 0이 된다.(6 = 3x2+0) 6은 2를 3개 가진 수이다. 몫인 3이 2의 2승 자리로 올라간다. 1의 자리에서 올라왔던 12는 2의 1승을 6개 가지고 있는 수이기도 하지만(12 = 2x6), 2의 2승을 3개 가지고 있는 수이기도 하다(12 = 4x3).

2의 2승 자리에 있는 3은 2보다 크므로 한번 더 자리올림이 발생한다. 3을 2로 나누면 몫은 1, 나머지는 1이다.(3 = 1x2+1) 몫인 1은 다음 자리인 2의 3승 자리로 올라가고 나머지 1은 2의 2승 자리에 남는다. 2의 3승 자리에 올라간 1은 2보다 작기 때문에 자리올림이 발생하지 않는다.
위의 과정을 통하여 10진수 13은 2진수 1101로 표현할 수 있다는 것을 알았다. 아래와 같이 검토해 보면 2진수 1101이 10진수 13이라는 것을 알 수 있다.

진법 변환에 대해 찾아보면 아래의 방법이 많이 보인다. 13을 더 이상 나눌 수 없을 때까지 나누는 것이다. 위 과정을 생각해 보면 아래 식의 원리가 이해되지 않을까 한다.

위 이미지 왼쪽의 나누기 계산에서 최종 몫부터 최초의 나머지까지 거꾸로 올라가면서 숫자를 나열해 보자. 10진수 13이 2진수로 표현되었다.
아래 이미지는 위 과정을 한꺼번에 나타낸 것이다.

아래와 같은 방식으로도 생각해 보았다.
13은 2의 4승보다는 작고 2의 3승보다는 크다.(16 > 13 > 8) 13을 8로 나누면 몫은 1, 나머지는 5이다. 13은 8을 1개, 5를 1개 가지고 있는 수다. 즉 2의 3승을 1개 가지고 있다.

5는 2의 3승보다는 작고 2의 2승보다는 크다.(8 > 5 > 4) 5를 4로 나누면 몫은 1, 나머지는 1이다. 5는 4를 1개, 1을 1개 가지고 있는 수다. 즉, 2의 2승을 1개 가지고 있다.

1은 2의 2승보다 작고 2의 1승보다도 작다. 1은 2의 1승을 가지고 있지 않다.

한꺼번에 보면 아래와 같다.

- 10진수 5861 → 16진수 변환
위와 같은 방법으로 10진수 5861을 16진수로 변환해 보았다. 위에서 과정을 모두 설명하였으니 아래에는 과정만 적어둔다.

10진법 5861이 16진법 16E5로 표현된다는 것을 알았다. 아래 과정을 통해 검토해 보자.

원하는 결과가 나왔다.
위에서 했던 것처럼 또 다른 방식도 생각해 보았다.

- 2진법 ↔ 16진법
2진법을 16진법으로 16진법을 2진법으로 하는 변환은 쉽다. 16진수 한 자리가 2의 4승과 일대일 대응하기 때문이다. 아래의 내용은 좀 길지만 일대일 대응한다는 한 가지의 개념을 풀어놓은 것뿐이다.
- 1~4자리 2진수 → 1자리 16진수
1~4자리의 2진수로 표현할 수 있는 값의 범위는 0000~1111(= 0~1111)이다. 0000(2)은 10진수로 0, 16진수로 0이다. 1111(2)은 10진수로 15, 16진수로 F이다. 따라서 2진수로 0000~1111은 16진수로 0~F이다. 2진수 1111에서 1이 증가한 10000은 16진수로 10이다. 2진수 4자리가 5자리가 되자 16진수에서도 똑같이 자리올림이 발생하였다. 16진수 한자리가 2진수 4자리와 일대일 대응하고 있다는 것을 알 수 있다.

그러므로 1~4자리 2진수는 10진수로 변환하는 방식으로 계산한 뒤 그 값을 바로 16진수로 변환해 주면 된다. 예를 들어 2진수 1101은 16진수로 아래와 같이 표현할 수 있다.

1011(2) = D(16)라는 결과가 나왔다. 4자리 2진수로 나올 수 있는 최댓값이 15(10)이다. 10진수를 2진수로 변환하는 과정이 익숙해진다면 4자리 2진수→1자리 16진수 변환은 간단히 암산할 수 있게 될 것이다.
- 1자리 16진수 → 1~4자리 2진수
1~4자리 16진수를 2진수로 표현해도 마찬가지다. 16진수 8을 2진수로 변환해 보자. 16진수 8은 10진수로도 8이다. 몫과 나머지 연산을 통해 10진수 8을 2진수로 변환해 보면 아래와 같이 나타난다.

8(16) = 1000(2)라는 결과가 나왔다. 사실 한자리 16진수는 위 연산을 하지 않고 간단한 암산으로도 2진수를 구할 수 있다. 8은 2의 3승이 1개 있는 수이다. 4자리 2진수에서 맨 앞자리가 2의 3승의 자리이므로 2의 3승 자리에 1, 나머지 자리에 0을 써주면 된다. 8(16) = 1000(2)이다. 아래와 같다.

16진수 B도 마찬가지로 몫과 나머지 연산을 통해 2진수를 구할 수 있다. 사실 16진수는 9를 초과하면 알파벳으로 표현된다는 게 약간 헷갈리고 생소하다. 이 부분만 익숙해지면 괜찮다.

B(16) = 1011(2)라는 결과가 나왔다. 이 또한 어렵지 않게 암산할 수 있다. B(16)은 11(10)이다. 11은 2의 3승 1개와 3으로 쪼개진다. 3은 다시 2의 1승 1개와 1로 쪼갤 수 있다. 4자리 2진수의 첫 번째 자리는 2의 3승의 자리이므로 첫 번째 자리에 1, 앞에서 3번째 자리(뒤에서 2번째 자리)는 2의 1승 자리이므로 해당 자리에 1, 마지막 1의 자리에 1을 적어주면 된다. 그 내용은 아래와 같다.

- 5~8자리 2진수 → 2자리 16진수
8자리의 2진수를 16진수로 표현하려면 어떻게 해야 할까? 1~8자리 2진수 표현범위는 00000000~11111111(= 0~11111111)이다. 10진수로 보면 0~255이다. 1~2자리 16진수 표현범위는 0~FF이다. FF는 10진수로 255이다. 8자리 2진수와 2자리 16진수는 표현범위가 같다.

앞서 4자리 2진수를 1자리 16진수로 표현하면 된다는 것을 확인했다. 5~8자리 2진수는 뒤 4자리, 나머지 앞자리를 각각 16진수로 변환해 이어 적어주면 된다. 아래 예시를 보자. 7자리 2진수 1010001(2)을 16진수로 변환해 보았다.

뒤 4자리인 0001을 1로, 앞에 남은 3자리를 5로 변환하여 이어 적으니 16진수 51이 되었다. 검토해 보면 1010001(2)은 10진수로 81, 51(16)도 10진수로 81이다.
8자리 2진수 11100101을 16진수로 변환해 보았다.

뒤 4자리인 0101(2)은 5(16)로, 앞 4자리 1110(2)은 E(16)로 변환하여 11100101(2) = E5(16)이 되었다. 11100101(2) = 229(10), E5(16) = 229(10)으로 옳게 계산되었다는 것을 확인할 수 있다.
5~8자리 2진수에서 뒤 4자리는 앞서 말한 대로 0~F까지 16진수 1자리와 일대일대응한다. 아래 8자리 2진수를 표현한 이미지를 보자. 8자리 2진수에서 뒤에서 5번째(앞에서 4번째) 자리는 2의 4승의 자리이다. 2의 4승은 2의 0승 x 2의 4승이다. 마찬가지로 2의 5승은 2의 1승 x 2의 4승이며, 2의 6승 = 2의 2승 x 2의 4승, 2의 7승 = 2의 3승 x 2의 4승이다. 모두 2의 4승을 가지고 있다.

이들을 2의 4승으로 묶으면 (2의 0승 ~ (2의 3승 + 2의 2승 + 2의 1승 + 2의 0승)) x 2의 4승이 된다. 괄호 안의 수의 범위는 16진수로 0~F가 된다. 따라서 앞 4자리는 (0~F) x16이다. 이는 16진수의 뒤에서 2번째 자리와 일대일 대응된다. 따라서 5~8자리 2진수는 뒤 4자리, 남은 앞자리를 각각 16진수로 변환해 이어주면 된다.
- 2자리 16진수 → 5~8자리 2진수
2자리 16진수를 2진수로 변환하는 것도 모두 위와 같다. 따라서 A6(16)을 2진수로 변환하는 예시만 적어둔다.

위와 같이 몫과 나머지 연산으로 자리마다 2진수를 구한 뒤 이어 붙여주면 된다.

위와 같이 간단한 암산으로(식은 길어 보이지만 실제로 암산해 보면 그렇지 않다.) 각 자리의 2진수를 구한 뒤 이어 붙여주면 된다. 한 가지 주의할 점은 두 자리 16진수 중 뒷자리를 2진수로 변환했을 때 3자리, 2자리, 1자리가 된다면 반드시 앞에 0을 추가하여 4자리로 만들어주어야 한다. 그래야 앞의 2진수들이 올바른 2의 n승의 위치에 자리할 수 있다.
- 9자리 이상의 2진수 ↔ 3자리 이상의 16진수
더 큰 자릿수의 2진수도 모두 앞서 설명한 것과 같은 원리로 변환해 주면 된다. 맨 뒤부터 4자리씩 끊어준다. 각각을 16진수로 변환한 뒤 순서대로 이어 붙이면 된다.

반대의 경우도 앞서 본 내용과 같다. 16진수를 1자리씩 끊어 각각 2진수로 변환한다. 맨 앞자리 16진수를 제외한 나머지는 4자리가 아니라면 0을 이용해 모두 4자리로 만든다. 얻은 값을 모두 이어 붙여준다.

아래와 같은 원리다.

- 2진법 ↔ 8진법
2진수 ↔ 8진수 변환 과정은 2진수 ↔ 16진수 변환 과정과 원리가 동일하다. 2진수 → 8진수 변환에서는 2진수를 뒤에서부터 3자리씩 끊은 뒤 각각 변환해 이어 붙이면 된다. 8진수 → 2진수 변환에서는 8진수 한 자리씩 각각 2진수로 변환한 뒤 이어 붙여주면 된다. 이때 맨 앞자리 8진수를 제외하고는 모두 2진수로 변환한 뒤 각각을 3자리를 만들어 붙여주어야 한다는 것을 주의하자. 2진수로 변환한 수가 2자리 또는 1자리 또는 0자리라면 0을 앞에 추가해 총 3자리로 만들어야 한다는 것이다.
여담
엑셀에 진법변환 함수가 존재하는데, 이름이 직관적이라 재미있다. 위 0-30의 진법변환표를 만들면서 알게 되었다. 영어로 2진법은 binary, 8진법은 octal, 10진법은 decimal, 16진법은 hexadecimal이다. 2진수를 줄여서 bin으로 표기한다. 2진수를 다른 진법으로 변환하고 싶을 땐 BIN2~ 인 함수를 사용하면 된다. 함수명이 '2진수 to ~'인 것이다. 함수들은 아래와 같다.
BIN2OCT : 2진수를 8진수로
BIN2DEC: 2진수를 10진수로
BIN2HEX: 2진수를 16진수로
8진수, 10진수, 16진수도 마찬가지다.
OCT2BIN: 8→2 / OCT2DEC: 8→10 / OCT2HEX: 8→16
DEC2BIN: 10→2 / DEC2OCT: 10→8 / DEC2HEX: 10→16
HEX2BIN: 16→2 / HEX2OCT: 16→8 / HEX2DEC: 16→10
댓글